Hukum kosinus, atau disebut juga
aturan kosinus, dalam
trigonometri adalah aturan yang memberikan hubungan yang berlaku dalam suatu
segitiga, yaitu antara panjang sisi-sisi segitiga dan
kosinus dari salah satu
sudut dalam segitiga tersebut.
Perhatikan gambar segitiga di kanan.
Aturan kosinus menyatakan bahwa

dengan

adalah sudut yang dibentuk oleh sisi
a dan sisi
b, dan
c adalah sisi yang berhadapan dengan sudut

.
Aturan yang sama berlaku pula untuk sisi
a dan
b:


Dengan kata lain, bila
panjang dua sisi sebuah segitiga dan sudut yang diapit oleh kedua sisi tersebut diketahui, maka kita dapat menentukan panjang sisi yang satunya. Sebaliknya, jika panjang dari tiga sisi diketahui, kita dapat menentukan besar sudut dalam segitiga tersebut. Dengan mengubah sedikit aturan kosinus tadi, kita peroleh:

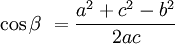




Hukum Kosinus Kedua



 adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut
adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut  .
.
 adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut
adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut  .
.


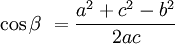







Tidak ada komentar:
Posting Komentar